Aggregate-Disaggregate Intermittent Demand Approach (ADIDA)
In previous tutorials we've looked at Croston's Method and a few adaptations which all seek to handle intermittent demand. The Aggregate-Disaggregate Intermittent Demand Approach (ADIDA) aims to remove intermittence by reducing a series into 'time-buckets'. For example, instead of analysing the daily sales, we sum the data into weekly sales and potentially remove or at least reduce the intermittence.

This allows a range of forecasting models to be utilised that would otherwise suffer from intermittency, such as Simple Exponential Smoothing.
After a forecast is made using one of these methods, the disaggregate part of ADIDA is breaking the series back down into the original time index. If you aggregated from daily to weekly, you might then divide the weekly forecast by seven to get it back down to daily. This would be an equal weight approach. But perhaps your demand tends to be higher on Saturdays, so you could also disaggregate with a higher weighting on that day.
ADIDA is a framework and different options for aggregating and disaggragating will be explored.
Aggregation - Overlapping and Non-overlapping
There are two choices that can be made when it comes to aggregating a time series - overlapping and non-overlapping. If you were to choose the time buckets in the above example, this would be consecutive non-overlapping as each of the sales fall into only one specified bucket. But you could also use overlapping buckets. Instead of jumping to the next seven day interval, you would step only one day forward and collect another bucket.
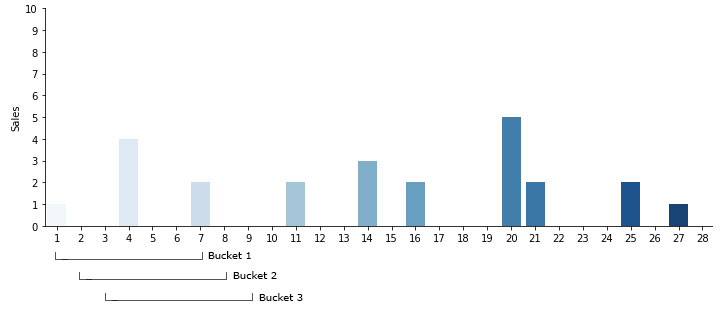
Choosing the Bucket Size
Remember that the goal of ADIDA is to reduce or remove intermittence. This means that ideally we need a large enough bucket to capture at least one sale so that the bucket becomes non-zero. To explore this, we'll use the M5 dataset, specifically the sales_train_validation.csv file.
import numpy as np
import pandas as pd
# Import data
sales = pd.read_csv('data/sales_train_validation.csv')
sales = sales.filter(like='d_').values
Let's iterate through each time series and collect the period between each demand occurence, joining them into one long array. We can then use numpy.quantile() to check different quantiles.
periods = []
for i in range(len(sales)):
ts = np.trim_zeros(sales[i,:], 'f')
p_idx = np.flatnonzero(ts)+1
p = np.diff(p_idx)
periods.append(p)
q = [0.5,0.75,0.95, 0.99]
periods = np.concatenate(periods)
q_results = np.quantile(periods, q)
for i in range(len(q)):
print(f'Quantile: {q[i]}, Bucket Size: {q_results[i]}')
print(f'\nMax interval: {periods.max()}')
If we want to capture 95% of the elements in entire M5 dataset, we will need a bucket size of seven days. If we want to push that to 99%, we need to extend that bucket to 18 days. The largest interdemand period is 1771 days, we certainly don't want to a use a bucket that large as we would lose all the information.
A good jumping off point might be looking at a seven day bucket.
ADIDA - The Step by Step Process
Non-overlapping
Let's start with non-overlapping buckets, where we will split the time series into buckets of equal size. First, we will plot the initial row in the M5 dataset.
import matplotlib.pyplot as plt
plt.figure(figsize=(16,4))
plt.plot(sales[0,:])
plt.show()
We want the time series to be a multiple of the bucket size so that it can be divided up equally and summed. We can do this by trimming the first few values from the beginning of the time series, then reshaping into an array of size (rows, bucket size). A row-wise summation will then produce the aggregated series.
ts = sales[0,:]
## Aggregate time series using bucket size of 7
size = 7
trim = len(ts) % size
ts_agg = ts[trim:].reshape(-1,size).sum(axis=1)
ts_agg = np.trim_zeros(ts_agg, 'f')
# Plot the aggregated series
fig, ax = plt.subplots(figsize=(16,4))
plt.title('Aggregated Series (Non-overlapping)')
plt.ylabel('Aggregated Sales')
plt.xlabel('Bucket Number')
plt.plot(ts_agg)
plt.show()
Visually, we can see that the intermittence has almost been removed, except for a short period near the middle. Choosing a larger bucket could eliminate that, but at the cost of smoothing over some of the frequencies that we may want to keep.
Overlapping Buckets
Aggregation with over-lapping buckets uses a sliding window. For this, we can use Numpy's convolve(). The function will take our time series and slide an array across it whilst doing an element-wise multiplication. So we set our sliding window to be an array of ones, eg in the case of a seven day window it will be [1,1,1,1,1,1]. Just a note that np.convolve reverses the sequence of the window, but since our window is all ones it won't change the result.
ts = np.trim_zeros(sales[0,:], 'f')
# Aggregation using a sliding window
size = 7
ts_agg = np.convolve(ts, np.ones(size), 'valid')
# Plot the aggregated series
plt.figure(figsize=(16,4))
plt.title('Aggregated Series (Overlapping)')
plt.ylabel('Aggregated Sales')
plt.xlabel('Bucket')
plt.plot(ts_agg)
plt.show()
Step 2: Make a Prediction
Now that we have our aggregated series, we can produce a forecast. For now, we will keep things simple and use a Naive forecast, which will just take the final value in the aggregated series. Later on we will test Croston's method.
pred = ts_agg[-1]
print(f'Prediction (Aggregated): {pred}')
The forecast of our aggregated series is 8 units. We will need to disaggregate this back down into the original time index.
Step 3: Disaggregation
Equal Weighted
The first option is an equal weighted disaggregation, where we simply divide the forecast by the number of days in our bucket.
forecast = pred / size
print(f'Forecast (Daily): {forecast:.3f}')
Seasonally Weighted
We can also do a seasonal disaggregation. This will involve going back to the original series and summing the sales for each day of the week. The proportion of total sales that each day represents can then be calculated.
ts = sales[0,:]
trim = len(ts) % 7
ts = ts[trim:]
s = ts.reshape(-1,7).sum(axis=0)
s_perc = [i/s.sum() for i in s]
print('Total sales: ', s)
print('Weights: ', np.around(s_perc,2))
We now have an array of percentages that can by multiplied with the single point forecast we made before.
forecast = [i * pred for i in s_perc]
print(np.around(forecast,2))
This will be the forecast for the next seven days of sales.
ADIDA Class
The procedure outlined so far has been put into the class below. Create an instance of the class with a time series, ts, using Adida(ts). The series can be aggregated calling the agg() method and passing values for the bucket size and whether or not an overlapping window should be used.
A forecasting function of your choice can then be passed to the predict() method to create a single point forecast from the aggregated series. Alternatively, a point forecast can be passed to the disagg() method along with parameters for the forecasting horizon and seasonality.
class Adida():
def __init__(self, ts):
# check shape first
self.ts = np.array(ts)
def agg(self, size=7, overlapping=False):
"""
Aggregate self.ts into "buckets", with an overlapping
or non-overlapping window
Parameters
----------
size : int
Size of aggregation window
overlapping : bool
Overlapping or non-overlapping window
"""
self.size = size
if overlapping:
ts_agg = np.convolve(ts, np.ones(self.size), 'valid')
else:
trim = len(self.ts) % self.size
ts_trim = self.ts[trim:]
ts_agg = ts_trim.reshape((-1, self.size)).sum(axis=1)
self.agg_ = np.trim_zeros(ts_agg, 'f')
return self
def predict(self, fn, *args, **kwargs):
"""
Helper function, pass a forecasting function whose first parameter is
the input time series. The aggregated time series will be passed to
this function followed by any arguments. The forecasting function must
return a single point forecast.
Parameters
----------
fn : function
Forecasting function
"""
self.pred = fn(self.agg_, *args, **kwargs)
return self
def disagg(self, prediction=None, h=7, seasonal=False, cycle=None):
"""
Disaggregate a prediction
Parameters
----------
prediction : optional
Pass a single point prediction if the predict() method hasn't
been used to generate a forecast
h : int
Forecasting horizon, number of periods to forecast
seasonal : bool
Seasonal disaggregation if True, equal weighted if False
cycle : int
Number of periods in the seasonal cycle of the input time series
Returns
-------
forecast : ndarray
1-D array of forecasted values of size (h,)
"""
if prediction is not None:
self.pred = prediction
if seasonal:
if not cycle:
raise ValueError('Seasonal disaggregation requires seasonal cycle number')
trim = len(self.ts) % cycle
s = self.ts[trim:].reshape(-1, cycle).sum(axis=0)
s_perc = [s.sum() and i/s.sum() for i in s] # Short-circuit for zero division
pred = self.pred * (cycle/self.size)
return np.resize([i * pred for i in s_perc],h)
else:
return np.array([self.pred/self.size] * h)
Croston's Method and the RMSSE
We'll continue looking at the M5 dataset, which was supplied from a competition hosted by Kaggle. The competition used the WRMSSE as the accuracy metric, which is built upon the RMSSE. To guage the accuracy of our ADIDA model, we'll use the RMSSE, which can be calculated with the function below.
def rmsse(train, test, forecast):
"""
Return RMSSE of a 1-D train and test set.
Forecast can be a single point value.
"""
forecast_mse = np.mean((test-forecast)**2)
train_mse = np.mean((np.diff(train)**2))
return np.sqrt(forecast_mse/train_mse)
Croston's method will be used to calculate a single point forecast for each aggregated series.
def croston(ts, alpha=0.1):
"""
Perform Croston's method on a time series, ts, and return
a single point forecast. Input time series is trimmed to
first non-zero element.
Parameters
----------
ts : array_like
1-D input array
alpha : float
Smoothing factor, `0 < alpha < 1`, default = 0.1
Returns
-------
forecast : float
Single point forecast
"""
z = ts[ts != 0]
ts_trim = np.trim_zeros(ts, 'f')
p_idx = np.flatnonzero(ts_trim)
p = np.diff(p_idx, prepend=-1)
n = len(z)
z_hat = np.zeros(n)
p_hat = np.zeros(n)
z_hat[0] = z[0]
p_hat[0] = np.mean(p)
for i in range(1,n):
z_hat[i] = alpha*z[i] + (1-alpha)*z_hat[i-1]
p_hat[i] = alpha*p[i] + (1-alpha)*p_hat[i-1]
forecast = z_hat / p_hat
return forecast[-1]
Let's grab a quick baseline RMSSE for Croston's method without using the ADIDA approach. Sticking with the gist of the Kaggle competition, we'll use the final 28 days as a test set.
train = sales[:,:-28]
test = sales[:,-28:]
rmsse_ = []
for row in range(len(sales)):
ts = train[row,:]
f = croston(ts, alpha=0.3)
rmsse_.append(rmsse(ts, test[row,:], f))
rmsse_mean = np.mean(rmsse_)
print(f'Croston RMSSE Baseline: {rmsse_mean:.3f}')
M5 Dataset and the Bucket Size
We'll iterate through a range of bucket sizes to see the effect on the RMSSE. For each bucket size, we'll use the Adida class to aggregate a row in the M5 dataset, calculate a forecast using Croston's method and then disaggregate using a 7-day seasonal cycle. The RMSSE will then be calculated and stored, before repeating this process for the next row. Once all rows have been calculated, the mean of all the RMSSE values will be taken.
buckets = [1,3,5,7,14,20,28,50,100,200]
rmsse_vals = []
for b in buckets:
rmsse_ = []
for row in range(len(train)):
ts = train[row,:]
f = (Adida(ts)
.agg(size=b, overlapping=False)
.predict(croston, alpha=0.3)
.disagg(h=28, seasonal=True, cycle=7)
)
rmsse_.append(rmsse(ts, test[row,:], f))
rmsse_vals.append(np.mean(rmsse_))
We can now plot the mean RMSSE for each bucket size tested.
plt.figure(figsize=(12,5))
plt.plot(buckets, rmsse_vals, label='Crostons Method, alpha=0.3')
plt.legend()
plt.xticks(buckets)
plt.xlabel('Bucket Size')
plt.ylabel('RMSSE mean')
plt.show()
The first value with a bucket size of one means had no aggregation. The resulting RMSSE was a slight improvement over the 0.95 baseline, due to the effect of the seasonal disaggregation. We then see some improvement as the bucket size increases and reaches 14 days, after which the error begins to rise in tandem with the size. If we could only pick one bucket size for the whole dataset, then we would choose a value around 14 days. But perhaps different products within the dataset perform better with a different bucket size. So we can dig a little deeper.
A Closer Inspection
Let's iterate through the first few rows and check the RMSSE for different sized aggregations.
def get_errors(row):
ts = sales[row,:-28]
test = sales[row,-28:]
errors = []
for b in buckets:
f = (Adida(ts)
.agg(size=b)
.predict(croston, alpha=0.3)
.disagg(h=28, seasonal=True, cycle=7)
)
err = rmsse(ts, test, f)
errors.append(err)
return errors
buckets = np.arange(1,100)
rows, cols = (3, 3)
fig, axs = plt.subplots(rows, cols, figsize=(4*cols,3*rows),
sharex=True)
for i in range(rows):
for j in range(cols):
errors = get_errors(3*i+j)
axs[i,j].plot(buckets, errors)
axs[i,j].set_title(f'Row={3*i+j+1}')
fig.supxlabel('Bucket Size')
fig.supylabel('RMSSE')
plt.tight_layout()
plt.show()
We can see that the behaviour is quite different for each series. Some series perform best at lower aggregation sizes, some at higher. So perhaps we can improve on our model by being more selective with the bucket size.
Optimising for Bucket Size
We can do a simple optimisation by choosing the aggregation level that reduces the RMSSE for each series. To do this, we'll create a validation set using the last 28 days of the training set. Below, we iterate through each row, create a forecast using each bucket size and find which one reduces the RMSSE when testing against the validation set. This bucket size is then stored in a list, optimal_size.
buckets = [1,2,3,5,7,10,14,28,50,100,200,365]
optimal_size = []
val = 28 # Validation set size
for row in range(len(train)):
rmsse_ = []
ts = train[row,:-val]
for b in buckets:
f = (Adida(ts)
.agg(size=b, overlapping=False)
.predict(croston, alpha=0.3)
.disagg(h=28, seasonal=True, cycle=7)
)
rmsse_.append(rmsse(ts, train[row,-val:], f))
optimal_size.append(buckets[np.argmin(rmsse_)])
Out of curiosity, we can check how many times each bucket size was selected.
# Plot the number of times each bucket size was selected
size, count = np.unique(optimal_size, return_counts=True)
plt.figure(figsize=(8,4))
plt.bar([str(x) for x in size], count)
plt.xlabel('Bucket Size')
plt.ylabel('Count')
plt.show()
Finally, we can check if this optimisation procedure produced any advantage over selecting just a 14-day aggregation level (RMSSE=0.912).
rmsse_vals = []
for row in range(len(train)):
ts = train[row,:]
f = (Adida(ts)
.agg(size=optimal_size[row], overlapping=False)
.predict(croston, alpha=0.3)
.disagg(h=28, seasonal=True, cycle=7)
)
rmsse_vals.append(rmsse(ts, test[row,:], f))
print(f'RMSSE: {np.mean(rmsse_vals):.3f}')
WRMSSE
For completeness, we can check the WRMSSE which will contain 28 days of unseen test data. The optimisation procedure will remain the same, except we will use the test set instead of the validation set. We will test three models, a vanilla Croston, a 14-day aggregation size and the optimised aggregation.
You can find the WRMSSE package here if you wish to run it locally, or install it with 'pip install m5-wrmsse'.
from m5_wrmsse import wrmsse
# No Aggregation, Seasonal Disaggregation
forecasts = []
for row in range(len(sales)):
ts = sales[row,:]
f = (Adida(ts)
.agg(size=1, overlapping=False)
.predict(croston, alpha=0.3)
.disagg(h=28, seasonal=True, cycle=7)
)
forecasts.append(f)
error = wrmsse(forecasts)
print(f'WRMSSE: {error:.3f}')
# 14-day Aggregation, Seasonal Disaggregation
forecasts = []
for row in range(len(sales)):
ts = sales[row,:]
f = (Adida(ts)
.agg(size=14, overlapping=False)
.predict(croston, alpha=0.3)
.disagg(h=28, seasonal=True, cycle=7)
)
forecasts.append(f)
error = wrmsse(forecasts)
print(f'WRMSSE: {error:.3f}')
# Optimised Aggregation, Seasonal Disaggregation
buckets = [1,2,3,5,7,10,14,28,50,100,200,365]
optimal_size = []
val = 28 # Validation set size
for row in range(len(sales)):
rmsse_ = []
ts = sales[row,:-val]
for b in buckets:
f = (Adida(ts)
.agg(size=b, overlapping=False)
.predict(croston, alpha=0.3)
.disagg(h=28, seasonal=True, cycle=7)
)
rmsse_.append(rmsse(ts, sales[row,-val:], f))
optimal_size.append(buckets[np.argmin(rmsse_)])
# Forecast using optimal sizes
forecasts = []
for row in range(len(sales)):
ts = sales[row,:]
f = (Adida(ts)
.agg(size=optimal_size[row], overlapping=False)
.predict(croston, alpha=0.3)
.disagg(h=28, seasonal=True, cycle=7)
)
forecasts.append(f)
error = wrmsse(forecasts)
print(f'WRMSSE: {error:.3f}')
The 14-day aggregation (WRMSSE=0.765) had only a slight improvement over no aggregation (WRMSSE=0.773). However, there was a significant improvement when optimising each series for the bucket size (WRMSSE=0.685).
Conclusion
In this tutorial we have explored the ADIDA procedure - aggregate a series, make a forecast and then disaggregate back down to the original time index. Using the M5 dataset, we looked at the performance of different aggregation sizes using the RMSSE as the accuracy metric. While a 14 day aggregation window minimised the mean RMSSE of the entire set, we found that each individual series varied quite differently in it's behaviour to the size. Optimising on a row-by-row basis lead to a final WRMSSE Of 0.685, where as casting a forecast using a static 14-day bucket resulted in an error of 0.765.
Instead of picking just one size, we could perhaps average multiple sizes. This idea is investigated further in the Intermittent Demand and Multiple Temporal Aggregation tutorial.