Adaptations of Croston's Method
The Syntetos-Boylan Approximation and the Teunter-Syntetos-Babai method are two adaptations of Croston's method that attempt to improve forecasting accuracy. This tutorial will run through the procedure for both methods and the advantages that come with using one of these methods. We'll then test both methods on a sample time series from the M5 dataset along with a methodology for parameter optimisation.
Syntetos-Boylan Approximation (SBA)
Syntetos & Boylan demonstrated that Croston's Method suffers from a positive bias. It over-estimates the forecast with a positive correlation to the smoothing factor for the demand interval, $\beta$. The larger the value for $\beta$ the stronger the positive bias. The Syntetos-Boylan Approximation introduces a modifcation to the forecast calculation, which attempts to reduce this bias. It is given by,
$$\hat{y}_t = (1 - \frac{\beta}{2})\frac{\hat{z}_{t}}{\hat{p}_t}$$Where, $\hat{y}_t$ is the forecast, $\hat{z}_{t}$ is the smoothed demand and $\hat{p}_t$ is the smoothed inter-demand period.
For example, if $\beta=0.1$, then the forecast is multiplied by a factor of $(1 - \frac{0.1}{2})=0.95$.
Teunter-Syntetos-Babai Method (TSB)
Another adaptation of Croston's Method is the Teunter-Syntetos-Babai Method (TSB). It also constructs two separate series, one for the demand and one for the demand probability.
$$ y_t > 0 \begin{cases} z_{t+1} = \alpha y_{t} + (1 - \alpha)z_{t} \\ p_{t+1} = \beta + (1 - \beta)p_{t} \\ \end{cases} $$When there is no demand,
$$ y_t = 0 \begin{cases} z_{t+1} = z_{t} \\ p_{t+1} = (1 - \beta)p_{t} \\ \end{cases} $$The forecast is then calculated as
$$\hat{y}_{t+1} = p_{t+1}*z_{t+1}$$The term $p_t$ is the probability of a demand occurence. For example, selling an item once every five days would equate to a $p_t$ of 0.2. The probability is then multiplied by the smoothed demand, $z_t$. A nice feature of TSB is that the forecast continues to update even when there isn't a demand occurence (unlike Croston and SBA, which predict the same value indefinitely). We'll see more on this a bit later.
Intermittent Demand Function
Below is some of the code taken from the Croston's Method tutorial with SBA and TSB added. The intmt_demand() function will return a forecast using the specified model (Croston, SBA or TSB). Values for the smoothing factors, $\alpha$ and $\beta$, can also be passed to the function.
import numpy as np
def intmt_demand(ts, method='cro', alpha=0.1, beta=0.1):
"""
Perform smoothing on an intermittent time series, ts, and return
a forecast array
Parameters
----------
ts : (N,) array_like
1-D input array
method : {'cro', 'sba', 'tsb'}
Forecasting method: Croston, Syntetos-Boylan Approximation
and Teunter-Syntetos-Babai method
alpha : float
Demand smoothing factor, `0 < alpha < 1`, default = 0.1
beta : float
Interval smoothing factor, `0 < beta < 1`, default = 0.1
Returns
-------
forecast : (N+1,) ndarray
1-D array of forecasted values
"""
# Initialise arrays for demand, z, and period, p. Starting
# demand is first non-zero demand value, starting period is
# mean of all demand intervals
ts_trim = np.trim_zeros(ts, 'f')
n = len(ts_trim)
z = np.zeros(n)
p = np.zeros(n)
p_idx = np.flatnonzero(ts)
p_diff = np.diff(p_idx, prepend=-1)
p[0] = np.mean(p_diff)
z[0] = ts[p_idx[0]]
if method in {'cro', 'sba'}:
q = 1
for i in range(1,n):
if ts_trim[i] > 0:
z[i] = alpha*ts_trim[i] + (1-alpha)*z[i-1]
p[i] = beta*q + (1-beta)*p[i-1]
q = 1
else:
z[i] = z[i-1]
p[i] = p[i-1]
q += 1
f = z / p
if method == 'sba':
f *= (1 - beta/2)
elif method == 'tsb':
p[0] = 1 / p[0] # Change to probability of demand occurence
for i in range(1,n):
if ts_trim[i] > 0:
z[i] = alpha*ts_trim[i] + (1-alpha)*z[i-1]
p[i] = beta + (1-beta)*p[i-1]
else:
z[i] = z[i-1]
p[i] = (1 - beta)*p[i-1]
f = p * z
nan_arr = [np.nan] * (len(ts)-n+1)
return np.concatenate((nan_arr, f))
An Advantage of TSB
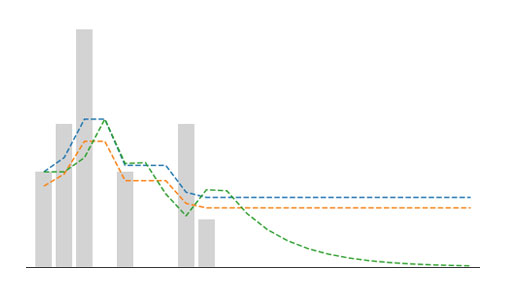
Let's look an example of a time series where sales fall and stay at zero. This could be a product going out of a fashion or becoming obsolete. We'll plot a forecast from Croston's method, SBA and TSB to see how each behave.
import matplotlib.pyplot as plt
ts = np.array([2,3,5,0,2,0,0,3,1,0,0,
0,0,0,0,0,0,0,0,0,0,0])
alpha, beta = 0.3, 0.3
fig, ax = plt.subplots(figsize=(9,5))
plt.bar(np.arange(len(ts)), ts, color='lightgrey', label='Actual')
for m in ['cro', 'sba', 'tsb']:
forecast = intmt_demand(ts, m, alpha, beta)
plt.plot(forecast, linestyle='--', label=m)
plt.xlabel('Time Index (t)')
plt.ylabel('Sales')
plt.legend()
plt.show()
Croston and SBA continue to forecast the same value since final demand, which is problematic. A retailer would not want to continue ordering a product if sales have dropped off cliff. As mentioned earlier, TSB will continues to update its prediction even when there is no demand occurence. This gives it an advantage of being responsive to periods of zero demand.
In the plot below, we can see that adjusting the value of $\beta$ can control how quickly the forecast will respond to a lack of demand.
betas = [0.05,0.5]
fig, ax = plt.subplots(figsize=(9,5))
plt.bar(np.arange(len(ts)), ts, color='lightgrey', label='Actual')
for b in betas:
forecast = intmt_demand(ts, 'tsb', 0.1, b)
plt.plot(forecast, linestyle='--', label=f'alpha=0.1, beta={b}')
plt.xlabel('Time Index (t)')
plt.ylabel('Sales')
plt.legend()
plt.show()
Optimising Parameters
To run through an example of optimising alpha and beta, we'll select a time series from the M5 dataset to use as an example. We'll use row index 5 and select the final 100 days of sales.
import pandas as pd
# Read in M5 dataset, select the final 100 days of row index 5
sales = pd.read_csv('data/sales_train_validation.csv')
ts = sales.iloc[5,-100:].values.astype('int')
# Plot sales series
plt.figure(figsize=(12,4))
plt.bar(np.arange(100), ts, color='lightgrey')
plt.xlabel('Time index')
plt.ylabel('Sales')
plt.show()
To be able to find the optimal parameters, we first need a cost function. We'll trial both the Mean Absolute Error and Mean Squared Error.
def mae(ts, forecast):
"Return mean absolute error of two numpy arrays"
return np.mean(np.abs(ts - forecast))
def mse(ts, forecast):
"Return mean squared error of two numpy arrays"
return np.mean((ts - forecast)**2)
Let's iterate through a range of values for alpha, create a forecast and check both the MAE and MSE. We'll store the error values in the dictionary named errors.
alphas = np.arange(0,1,0.02)
errors = {'MAE': [], 'MSE': []}
for a in alphas:
f = intmt_demand(ts, method='cro', alpha=a, beta=0.1)
idx = np.argmax(np.isfinite(f)) # Index of first non-NaN value
mae_error = mae(ts[idx:], f[idx:-1])
mse_error = mse(ts[idx:], f[idx:-1])
errors['MAE'].append(mae_error)
errors['MSE'].append(mse_error)
One of the drawbacks of using the MAE or MSE is that it can favour a zero-forecast. We'll check the error of a zero-forecast by passing the time series and a value of 0 to the mae() and mse() functions.
# Calculate errors when casting a zero-forecast
zero_mae = mae(ts, 0)
zero_mse = mse(ts, 0)
We'll now plot both errors as a function of alpha, along with the zero-forecast error.
# Plot errors as a function of alpha
fig, axs = plt.subplots(2, 1, figsize=(8,8))
axs[0].plot(alphas, errors['MAE'], label='MAE')
axs[0].axhline(zero_mae, color='red', linewidth=0.5,
linestyle='--', label='Zero Forecast')
axs[0].set_yticks(np.arange(0.6,2,0.2))
axs[0].legend()
axs[1].plot(alphas, errors['MSE'], label='MSE')
axs[1].axhline(zero_mse, color='red', linewidth=0.5,
linestyle='--', label='Zero Forecast')
axs[1].set_yticks(np.arange(2,4.4,0.4))
axs[1].legend()
fig.supxlabel('Alpha')
fig.supylabel('Error')
plt.tight_layout()
plt.show()
From the plots, we can see both error measures are minimised when alpha is around 0.1 to 0.2. Note that simply forecasting zero produces a lower MAE than any of the forecasts. This illustrates a problem using MAE for gauging the accuracy of a forecast. While a forecast of zero would minimise the MAE, in the real world this translates to ordering no stock which would result in empty shelves in the store. In this case, the forecasts produced a lower MSE than the zero-forecast, but the MSE will also suffer from the same issue for certain series.
Alternative measures of accuracy are discussed in another tutorial, Error Metrics for Intermittent Demand. For now, we'll push on using the MSE and look at how we can use the minimize() function from the scipy library.
Optimisation with scipy.optimise.minimize()
The min_error_func() below takes in the parameters we want to optimise (alpha, beta), makes a forecast, then returns the error between that forecast and the original time series. Scipy's minimize() function will then attempt to minimise the output of min_error_func() by adjusting the values for alpha and beta.
We'll test it out using TSB as the forecasting model and the MSE as the error metric.
from scipy.optimize import minimize
def min_error_func(params, ts, method, metric=mae):
alpha, beta = params
f = intmt_demand(ts, method=method, alpha=alpha, beta=beta)
idx = np.argmax(np.isfinite(f))
return metric(ts[idx:], f[idx:-1])
# Find optimal values for alpha, beta using the MSE as the
# error metric, and TSB as the forecasting model
init = [0.1,0.1] # Initial guess for alpha, beta
tsb_opt = minimize(min_error_func, init,
args=(ts, 'tsb', mse),
bounds=[(0,1), (0,1)])
print(f'Optimal alpha: {tsb_opt.x[0]:.4f}')
print(f'Optimal beta: {tsb_opt.x[1]:.4f}')
This can be repeated for both Croston's Method and SBA.
sba_opt = minimize(min_error_func, init,
args=(ts, 'sba', mse),
bounds=[(0,1), (0,1)])
print(f'Optimal alpha: {sba_opt.x[0]:.4f}')
print(f'Optimal beta: {sba_opt.x[1]:.4f}')
cro_opt = minimize(min_error_func, init,
args=(ts, 'cro', mse),
bounds=[(0,1), (0,1)])
print(f'Optimal alpha: {cro_opt.x[0]:.4f}')
print(f'Optimal beta: {cro_opt.x[1]:.4f}')
We can now create a forecast using the optimal values found. We'll do this for Croston's method, SBA and TSB and then plot the forecast along with the original time series.
# Forecast using optimal values of alpha and beta
f_tsb = intmt_demand(ts, 'tsb', tsb_opt.x[0], tsb_opt.x[1])
f_sba = intmt_demand(ts, 'sba', sba_opt.x[0], sba_opt.x[1])
f_cro = intmt_demand(ts, 'cro', cro_opt.x[0], cro_opt.x[1])
# Plot results
plt.figure(figsize=(12,5))
plt.bar(np.arange(100),ts, color='lightgrey')
plt.plot(f_tsb, linestyle='--', label='TSB')
plt.plot(f_sba, linestyle='--', label='SBA')
plt.plot(f_cro, linestyle='--', label='CRO')
plt.xlabel('Time index')
plt.ylabel('Sales')
plt.legend()
plt.show()
Conclusion
So far we've covered Croston's method and the SBA and TSB adaptations. We've optimised parameter selection using MSE, but have noted that it can suffer from a bias towards a zero-forecast. This translates poorly into real-world scenarios as it would mean it could leave shelves empty of stock.
Different approaches to measuring accuracy are explored in the Error Metrics for Intermittent Demand tutorial, where we look at metrics such as the Periods in Stock and the Cumalative Forecasting Error.
Alternatively, we can attempt to remove intermittence in the time series through aggregation methods. This is discussed further in the ADIDA tutorial.